树的插入（创建）为什么要使用指针的指针

Posted on | | Visitors:

一个二叉排序树的例子

首先看一个常见的二叉排序树的操作，下面的代码包括插入、创建和中序遍历。摘自这里。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<stdio.h>
#include<stdlib.h>

typedef int ElemType;
struct BTreeNode
{
	ElemType data;
	struct BTreeNode* left;
	struct BTreeNode* right;
};

//递归方式插入
void Insert(struct BTreeNode** BST, ElemType x)
{
	if (*BST == NULL) //在为空指针的位置链接新结点
	{
		struct BTreeNode* p = (BTreeNode*)malloc(sizeof(struct BTreeNode));
		p->data = x;
		p->left = p->right = NULL;
		*BST = p;
	}
	else if (x < (*BST)->data) //向左子树中完成插入运算
		Insert(&((*BST)->left), x);
	else
		Insert(&((*BST)->right), x); //向右子树中完成插入运算
}

//创建二叉搜索树，根据二叉搜索树的插入算法可以很容易实现
void CreateBSTree(struct BTreeNode** BST, ElemType a[], int n)
{
	int i;
	*BST = NULL;
	for (i = 0; i < n; i++)
		Insert(BST, a[i]);
}

void Inorder_int(struct BTreeNode* BT)//中序遍历,元素类型为int
{
	if (BT != NULL)
	{
		Inorder_int(BT->left);
		printf("%d,", BT->data);
		Inorder_int(BT->right);
	}
}

//主函数
void main()
{
	int x, *px;
	ElemType a[10] = { 30,50,20,40,25,70,54,23,80,92 };
	struct BTreeNode* bst = NULL;
	CreateBSTree(&bst, a, 10); //利用数组a建立一棵树根指针为bst的二叉搜索树

	printf("进行相应操作后的中序遍历为：\n");
	Inorder_int(bst);
	printf("\n");

	printf("输入待插入元素值：");
	scanf(" %d", &x);
	Insert(&bst, x);

	printf("进行相应操作后的中序遍历为：\n");
	Inorder_int(bst);
	printf("\n");
}

我一直很纳闷为什么插入（创建）操作需要传递指针的指针，不是指针就可以操作被指向的内容吗？为解决这个疑惑，首先看一下C语言的函数传参。

C语言函数传参

一个经典的例子就是交换两个数的值，swap(int a,int b)，大家都知道这样做a和b的值不会被交换，需要swap(int *a,int *b)。从函数调用的形式看，传参分为传值和传指针两种（C++中还有传引用）。实际上在C语言中，值传递是唯一可用的参数传递机制，函数参数压栈的是参数的副本。传指针时压栈的是指针变量的副本，但当你对指针解指针操作时，其值是指向原来的那个变量，所以可以对原来变量操作。

分析

再看一下前面的二叉树插入的例子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
BTreeNode *root=NULL; // STEP 1
Insert(&root,x);      // STEP 2

void Insert(struct BTreeNode** BST, ElemType x)
{
	if (*BST == NULL) 
	{
		struct BTreeNode* p = (BTreeNode*)malloc(sizeof(struct BTreeNode));   // STEP  3
 		p->data = x;
		p->left = p->right = NULL;
		*BST = p;     // STEP  4
	}

	...

}

函数递归调用，每次真正产生变化的时候传递进去的都是空指针。当树根为空时，我们图解看一下函数调用的值拷贝。

STEP

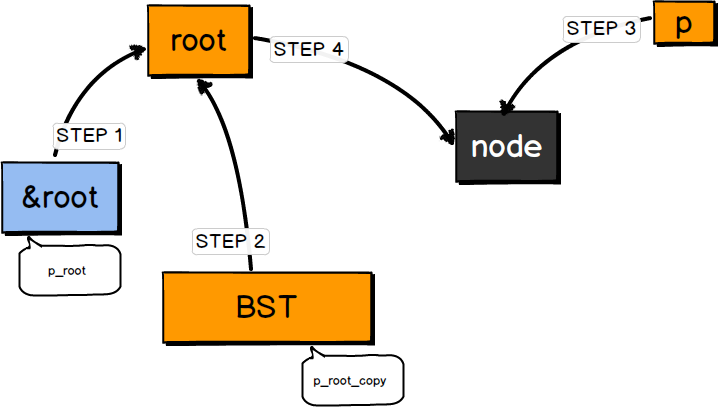
  • STEP 1 定义一个空指针root，&root为指针root的地址，图中的箭头表示指针的指向。

  • STEP 2 调用Insert，产生一个&root的拷贝BST，即BST指向root。

  • STEP 3 生成一个新的节点为node，由指针p指向node。

  • STEP 4 (*BST)=p，也就是root的值为p（node的地址），于是root指向了新生成的节点。

如果我们把函数与调用改成一级指针，看下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
BTreeNode *root=NULL; // STEP 1
Insert(root,x);      // STEP 2

void Insert(struct BTreeNode* BST, ElemType x)
{
	if (BST == NULL) 
	{
		struct BTreeNode* p = (BTreeNode*)malloc(sizeof(struct BTreeNode));   // STEP  3
 		p->data = x;
		p->left = p->right = NULL;
		BST = p;     // STEP  4
	}

	...

}

再图解一下调用过程。

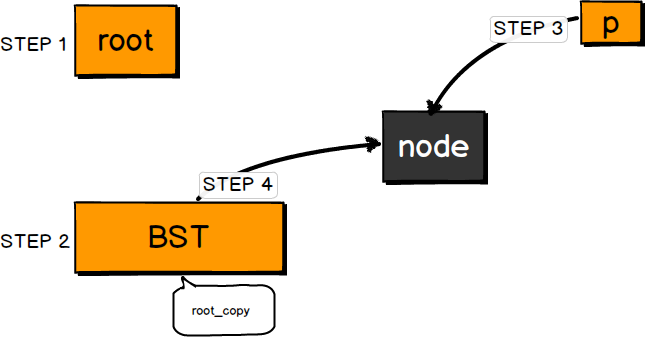
STEP2

  • STEP 1 定义一个空指针root。

  • STEP 2 调用Insert，产生一个root的拷贝BST，BST与root的值一样都为空，所以都没有指向。

  • STEP 3 生成一个新的节点为node，由指针p指向node。

  • STEP 4 BST=p，也就是BST的值为p（node的地址），于是BST指向了新生成的节点。

执行结束后我们得到了一个根节点但是root并没有指向这个节点。

那么能不能通过一级的指针就得到正确结果呢？答案是可以，看两个图的区别，其实就是root最后要指向node，即root=BST。所以只需要给函数加一个返回值，就可以通过一级指针得到同样的结果，看下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//调用
root = Insert_1(root,x);

//递归一级指针
BTreeNode* Insert_1(struct BTreeNode* BST, ElemType x)
{
	if (BST == NULL) 
	{
		struct BTreeNode* p = (BTreeNode*)malloc(sizeof(struct BTreeNode));
		p->data = x;
		p->left = p->right = NULL;
		BST = p;
	}
	else if (x < BST->data) //向左子树中完成插入运算
		BST->left = Insert_1(BST->left, x);
	else
		BST->right = Insert_1(BST->right, x); //向右子树中完成插入运算
	return BST;
}

结果正确：

output

但是从语义上看，一级指针的写法没有二级指针那么直观，遇到需要对树进行修改的操作时还是用二级指针更好一点。